Probability Calculator, Formulas & Solved Examples
getcalc.com's Probability Calculator is an online statistics & probability tool to estimate the possibility of single or multiple events to occur in statistical trials or experiments. Use this calculator to find the probability of independent, complement, mutual or non-mutual, union, intersection & condition probability of events.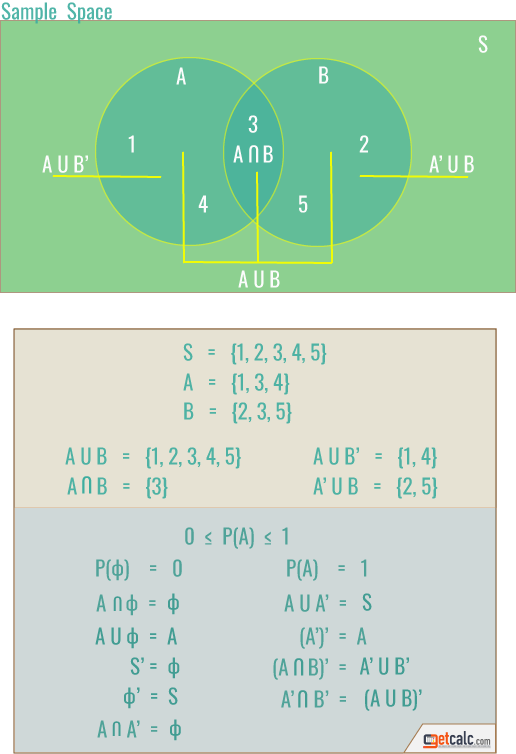
Probability is a mathematical function or method used in the context of probability & statistics represents the possibility of events to occur, generally measured by the ratio of favorable events to the total number of events possible. It is a study and interpretation of chance of outcomes in the sample space of statistical experiments. The probability of event in the sample space is always lies between 0 and 1, mathematically represented as (0 ≤ p(A) ≤ 1).
What is Sample Space?
The Sample Space of an statistical experiment is the set of all possible outcomes and is generally represented by an alphabet S. Each outcome of a sample space is called as element or member or sample point of a sample space.
What is an Event?
An Event is a subset of sample space.
What is a Complement of event?
The Complement of Event A is generally represented by A’ and is a subset of all elements or events of S that are not in A, and it can be calculated from
P(A’) = 1 - P(A)
What is an Independent Event?
In probability & statistics, if an event A is said to be independent then it does not affect the outcome of event B where A and B are the two events of sample space S. In other words, the product of probability of events A and B equals to probability of intersection of events A and B.
P(A ∩ B) = P(A) P(B)
Tossing a coin or throwing a dice are the examples of independent events.
What is Mutual Events?
The two events A and B are said to be mutual, if the sample space has at least one element in common to events A and B.
What is Mutually Exclusive Events?
The events are said to be disjoint or mutually exclusive, if two events A and B that can not both occur at the same time or it does not have any common elements. For example, it is not possible to get both HEAD & TAIL, when a coin is tossed.
(A ∩ B) = Φ
P(A ∩ B) = Φ
What is Intersection?
In probability & statistics, the Intersection of two events A and B in the sample space S is the events that are common to A and B, and is generally represented by A ∩ B.
(A ∩ B) = A x B
P(A ∩ B) = P(A) P(B)
What is Union?
In probability & statistics, the Union of two events A and B in the sample space S is all the events of A or B or both, and is generally represented by A U B.
(A U B) = A + B - (A ∩ B)
(A U B) = A + B
P(A U B) = P(A) + P(B) - P(A ∩ B)
P(A U B) = P(A) + P(B), if the events are mutually exclusive
What is conditional probability?
Conditional probability is the measure of probability of an event A given that the event of B has already occurred. In other words, its a possibility of expected event to occur based on the occurrence of previous event.
P(A|B) = P(A ∩ B)/P(B)
similarly,
P(B|A) = P(A ∩ B)/P(A)
Formulas to Remember

How to find all the outcomes of sample space for coin flips?
In probability theory, the probability is calculated for the favorable events to occur. It's generally the total number of ways for the favorable or expected event or events to occur divided by the the total outcomes of the sample space S. Refer the below tree diagram to find all the possible outcomes of sample space for flipping a coin one, two, three & four times. For more coin flips, the total outcomes of a trial get increased twice as the n - 1 time.
| Sample Space Tree Diagram for 4 Coin Tosses | ||||
| First Flip | Second Flip | Third Flip | Fourth Flip | Possible Events |
| H | H | H | H | HHHH |
| T | HHHT | |||
| T | H | HHTH | ||
| T | HHTT | |||
| T | H | H | HTHH | |
| T | HTHT | |||
| T | H | HTTH | ||
| T | HTTT | |||
| T | H | H | H | THHH |
| T | THHT | |||
| T | H | THTH | ||
| T | THTT | |||
| T | H | H | TTHH | |
| T | TTHT | |||
| T | H | TTTH | ||
| T | TTTT | |||
Probability of Events
Based on the design of experiments, the outcome of events can be classified as independent, complement, mutual, non-mutual, union, intersection & conditional probability of events. The best example for the probability of events to occur is flipping a coin or throwing a dice.
For flipping a coin,
the sample space of total outcomes
S = {H,T} where H & T corresponds to Head & Tail of a coin respectively
S = {2} for a single toss of a coin

the sample space of total outcomes
S = {1, 2, 3, 4, 5, 6}
S = 6
for showing odd or even numbers
S = {Even, Odd}
S = 2
Probability of Events
Based on the design of experiments, the outcome of events can be classified as independent, complement, mutual, non-mutual, union, intersection & conditional probability of events. The best example for the probability of events to occur is flipping a coin or throwing a dice.
For flipping a coin,
the sample space of total outcomes
S = {H,T} where H & T corresponds to Head & Tail of a coin respectively
S = {2} for a single toss of a coin

the sample space of total outcomes
S = {1, 2, 3, 4, 5, 6}
S = 6
for showing odd or even numbers
S = {Even, Odd}
S = 2
Complement of Event A
Complement of events A is the probability function which represents the subset of all members which are not present in A (event of not A) generally denoted by the symbol A'.
P(Ac) = 1 - P(A)
For example, the elements of sample space
S = {pen, pencil, eraser, sharpener, note, box}
If events of A = {pen, pencil, eraser, sharpener}
then the events of A' = {note, box}
By using this probability calculator, users may find the possibility of complement of events A of sample space S in the statistical experiments.
Use this probability calculator to find the possibility of complement of events A in the sample space S.
Mutually Exclusive Events A & B - Union & Intersection
In a sample space of statistical experiment, the mutually exclusive events A & B denoted by A ∩ B = null that represents that there is no elements of events A & B are in common.
The probability function of mutually exclusive events A & B
(A U B) = A + B
P(A U B) = P(A) + P(B)
For example, the elements of sample space
S = {1, 2, 3, 4, 5, 6}
Event A = {1, 2, 3}
Event B = {4, 5, 6}
(A ∩ B) = null = 0
By using this probability calculator, users may find the possibility of successful elements of mutually exclusive events A or B of sample space S in the statistical experiments.
Mutual Events A & B - Union & Intersection
In a sample space of statistical experiment, the union of events A & B denoted by A U B represents that there is the common elements of events A, B or both A & B.
The probability function of mutual events A & B
P(A U B) = P(A) + P(B) - P(A ∩ B)
For example, the elements of sample space
S = {1, 2, 3, 4, 5, 6}
Events of A = {1, 2, 3, 4}
Events of B = {3, 4, 5, 6}
(A ∩ B) = {3, 4}
A U B = {1, 2, 3, 4} + {3, 4, 5, 6} - {3, 4}
A U B = {1, 2, 3, 4, 5, 6}
By using this probability calculator to find the possibility of successful events A or B or both in the sample space S.
Example Probability Calculations
Users may refer the below solved example calculations to learn how to find what is the possibility of single or multiple independent, complement, mutual or non-mutual, union, intersection & condition probability of events to occur in statistical experiments.
Example Problem
What is the probability of getting 2 heads in 3 tosses of a coin?
Solution
Step by step workout :
For tossing a coin 3 times,
The elements of sample space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Expected element of Event A = {HHH, HHT, HTH, THH}
P(A) = ?
The total number of possible outcomes in a sample space for tossing a coin 3 times is 8.
The number of expected outcome from tossing a coin 3 times is 4.
Therefore,
P(A) = Number of Successful Events ÷ Total Events of Sample Space
= 2/8
= 0.5
P(A) = 0.5
0.5 is the probability of getting 2 heads in 3 tosses.
Example Problem
What is the probability for getting 5 when throwing a dice?
Solution
Step by step workout :
For a dice,
The total elements of sample space S = {1, 2, 3, 4, 5, 6}
Expected element of Event A = {5}
P(A) = ?
The total number of possible outcomes in a sample space for throwing a dice is 6.
Expected element of Event A is 1
Therefore,
P(A) = Number of Successful Events ÷ Total Events of Sample Space
= 1/6
= 0.16
P(A) = 0.16
0.16 is the probability of getting 5.
Example Problem
What is the probability for getting face card from the deck of cards?
Solution
Step by step workout :
For a getting a face card,
The elements of sample space S for a deck of cards = {spade (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), clubs (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), heart (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), diamond (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King)}
S = 52
Expected elements or face cards of Event A = {spade (Jack, Queen, King), clubs (Jack, Queen, King), heart (Jack, Queen, King), diamond (Jack, Queen, King)}
The total group is 4. Three face cards in each groups.
A = 3 x 4 = 12
P(A) = ?
The total number of possible outcomes in a sample space for a deck of cards is 52.
Expected elements of Event A is 12
Therefore,
P(A) = Number of Successful Events ÷ Total Events of Sample Space
P(A) = 12/52
= 3/13
= 0.23
P(A) = 0.23
0.23 is the probability of getting face card from a deck of cards.
Example Problem
What is the probability for getting Ace from the deck of cards?
Solution
Step by step workout :
For a getting a Ace card,
The events of sample space S for a deck of cards = {spade (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), clubs (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), heart (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King), diamond (Ace, 2, 3, 4, 5, 6, 7, 8, 9, Jack, Queen, King)}
S = 52
Expected elements or Ace of Events A = {spade Ace, clubs Ace, heart Ace, diamond Ace}
The total group is 4. One Ace card in each groups.
A = 1 x 4 = 4
P(A) = ?
For a single draw, the total number of possible outcomes or events in a sample space for a deck of cards is 52.
Expected events A is 4.
Therefore,
P(A) = Number of Successful Events ÷ Total Events of Sample Space
P(A) = 4/52
= 1/13
= 0.07
P(A) = 0.07
0.07 is the probability of getting Ace from a deck of 52 cards.
Example Problem
What is the probability of getting Ace, if the drawn Ace is not placed back in the deck.
Solution
Step by step workout :
If the drawn Ace is not placed back, the total number of possible outcomes or events in a sample space for a deck of cards is 51.
Expected events A is 3
Therefore,
P(A) = Number of Successful Events ÷ Total Events of Sample Space
P(A) = 3/51
= 1/17
= 0.058
P(A) = 0.058
0.058 is the probability of getting Ace from a deck of 51 cards.
Grade school students, teachers or professionals may use the above solved example calculations to learn how to solve the probability problems, and use this calculator to verify the answers or practice the worksheets or compute the different trials of statistical experiments to analyze the sample space and probability of events.

