Average of Fractions and Mixed Numbers Calculator
getcalc.com's Fractions and Mixed Numbers Average calculator is an online basic math function tool to find an equivalent fraction for the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. This calculator also featured to generate the complete work with steps for any given valid input values to assist elementary or grade school students to solve the fractions average worksheet or homework problems effectively. Users can generate the step by step calculation for the corresponding input values or verify the similar calculation results by using this fractions and mixed numbers average calculator.
Multiple Fractions Average and Formula
Average of Multiple Fractions is a basic arithmetic operation used to find the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. The below formula is the mathematical representation for average of multiple fractions with like or unlike denominators, positive or negative fractions or mixed or whole numbers.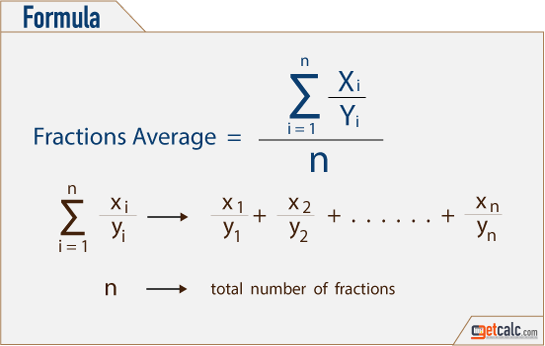
How to Find the Average of Two or More Fractions
The average of fractions is the sum of all fractions divided by the count of total number of fractional numbers. Any whole number in the group of fractions considered as a fraction with denominator 1. For fractions with same or equal denominators, the sum is the simplified fraction of sum of numerators divided by the common denominators, whereas, for fractions with unlike, unequal or different denominators, the LCM (least common multiple) of all denominators must be multiplied with both numerators and denominators of each fractions to bring the common denominator to perform the addition between them. By using this tool and associated information, users may refer the below solved examples with step by step calculation to learn how to find the average of two, three or more fraction numbers with same or different denominators, or the average of regular, irregular, positive or negative fractions and whole numbers. user may found the answers for the following queries
Average of Three Fractions with Different Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with unlike, unequal or different denominators.
Problem
Find the average of fractions 1/2, 1/3 and 1/4.
Step by step workout
step 1 Address formula and input values.
Input values:
1/2, 1/3 , 1/4
Total count = 3
(1/2 + 1/3 + 1/4)/3 = ?
step 2 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
12 is the LCM for 2, 3 and 4.
step 3 Multiply LCM 12 with each numerators and denominators
= (1 x 12)/(2 x 12) + (1 x 12)/(3 x 12) + (1 x 12)/(4 x 12)
step 4 Simplify the above expression to bring same denominators for all fractions.
= 6/12 +4/12+3/12
= (6 + 4 + 3)/12
step 5 Add all numerators and rewrite it in a single form.
= 13/12
1/2+1/3+1/4= 13/12
step 6 Divide the sum by total count of fractions.
(1/2 + 1/3 + 1/4)/3 = (13/12)/3
13/12is the average of three fractions 1/2, 1/3 and 1/4.
Average of Three Fractions with Same Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with same, equal or common denominators.
Problem
Find the average of fractions 5/9, 6/9 and 7/9.
Step by step workout
step 1 Address formula and input values.
Input values:
5/9,6/9,7/9
Total count = 3
(5/9 + 6/9 + 7/9)/3 = ?
step 2 Find the sum of all fractions.
(5 + 6 + 7)/9=18/9
=18/9
step 3 Divide the sum by total count of fractions and simplify
= (18/9)/3
(5/9 + 6/9 + 7/9)/3 = 2/3 in fraction form
(5/9 + 6/9 + 7/9)/3 = 0.66 in decimal form
2/3 or 0.66 is the average of three fractions 5/9, 6/9 and 7/9.
Average of Multiple Fractions and Whole Numbers
The below solved example with step by step workout may help users to learn how to find the average of multiple regular or irregular fractions with like or different denominators and whole numbers.
Problem
Find the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.
Step by step workout
step 1 Address formula and input values.
Input values:
2/3,3/4,6,4/5, 3 ,5/6,8/9
Total count = 7
2/3,3/4,6,4/5, 3 ,5/6,8/9 = ?
step 2 Convert whole numbers to fractions and rewrite as below
Any whole number or integer is a rational number (quotient of 1), hence the denominators for all whole numbers is 1 and can be written as
6 =6/1
3 =3/1
step 3 Arrange all the numbers as fractions
2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
180 is the LCM for 3, 4, 1, 5, 1, 6 and 9.
step 5 multiply LCM 180 with each numerators and denominators
=(2 x 180)/(3 x 180)+(3 x 180)/(4 x 180) +(6 x 180)/(1 x 180)+ (4 x 180)/(5 x 180)+(3 x 180)/(1 x 180)+(5 x 180)/(6 x 180)+(8 x 180)/(9 x 180)
step 6 simplify the above expression to bring same denominators for all fractions.
=120/180+135/180+1080/180+144/180+540/180+150/180+160/180
=(120 + 135 + 1080 + 144 + 540 + 150 + 160)/180
step 7 add all numerators and rewrite it in a single form.
=2329/180
=2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9=2329/180
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/7 = (2329/180)/7
= 2329/1260
2329/1260 is the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.
Average of Multiple Positive and Negative Fractions
The below solved example with step by step calculation may help users to learn how to find the average of multiple whole numbers, positive and negative fractions (with unlike or different denominators).
Problem
Find the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.
Step by step workout
step 1 Address formula and input values.
Input values:
2/3,2/4,-2/5, 6 ,2/7,-3/9
Total count = 6
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
6 = 6/1
step 3 Arrange all the numbers as fractions.
2/3+2/4+-2/5+6/1+2/7+-3/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
1260 is the LCM for 3, 4, 5, 1, 7 and 9.
step 5 Multiply LCM 1260 with each numerators and denominators
=(2 x 1260)/(3 x 1260)+(2 x 1260)/(4 x 1260)-(2 x 1260)/(5 x 1260)+(6 x 1260)/(1 x 1260)+(2 x 1260)/(7 x 1260)-(3 x 1260)/(9 x 1260)
step 6 Simplify the above expression to bring same denominators for all fractions.
=(2 x 420)/(1260)+(2 x 315)/(1260)-(2 x 252)/(1260)+(6 x 1260)/(1260)+(2 x 180)/(1260)-(3 x 150)/(1260)
=840/1260+ 630/1260- 504/1260 + 7560/1260 + 360/1260 - 450/1260
step 7add all numerators and rewrite it in a single form.
=(840 + 630 + 504 + 7560 + 360 + 450)/1260
=10344/1260
=862/105
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9) = 862/105
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/6 = (862/105)/6
= (431/105)/3
=431/315
431/315 is the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.
Average of Two or More Fractions and Mixed Numbers
The below solved example for average of two or more fractions, mixed numbers and whole numbers. The fraction numbers include regular, irregular, negative or positive fractions with same or unlike denominators. The below step by step work guides how to find equivalent fraction for the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Problem
Find the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Step by step workout
step 1 Address formula and input values.
Input values:
2/3,4/5,6/7, 3 8/9, 6 1/2, 9
Total count = 6
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
9 = 9/1
step 3 Convert the mixed fractions to fractions, if any
38/9= ((3 x 9) + 8)/9= 35/9
61/2= ((6 x 2) + 1)/2= 13/2
step 4 Arrange all the numbers as fractions.
2/3+4/5+6/7+35/9+13/2+9/1
step 5 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
630 is the LCM for 3, 5, 7, 9, 2 and 1.
step 6 Multiply LCM 630 with each numerators and denominators
=(2 x 630)/(3 x 630)+(4 x 630)/(5 x 630)+(6 x 630)/(7 x 630)+(35 x 630)/(9 x 630)+(13 x 630)/(2 x 630)+(9 x 630)/(1 x 630)
step 7 Simplify the above expression to bring same denominators for all fractions.
=(2 x 210)/(630)+(4 x 126)/(630)+(6 x 90)/(630)+(35 x 70)/(630)+(13 x 315)/(630)+(9 x 630)/(630)
=420/630+504/630+54/630+2450/630+4095/630+5670/630
step 8 Add all numerators and rewrite it in a single form.
=(420 + 504 + 54 + 2450 + 4095 + 5670)/630
=13193/630
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9) = 13193/630
step 9 Divide the sum by total count of fractions.
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = (13193/630)/6
=13193/3780
13193/3780 is the average of multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.

