4 Variables (Karnaugh's Map) K-Map Solver
getcalc.com's online 4 Variables K-map solver, table, grouping & work with steps to find the Sum of Products (SOP) or to minimize the given logical (Boolean) expressions formed by A, B, C & D based on the laws & theorems of AND, OR & NOT gates in digital electronics. This web based Karnaugh's map calculator tool is featured to generate the complete work with steps (including each grouping of 1s) for any corresponding input values of A, B, C & D or logical expressions formed by A, B, C, D, A, B, C & D. Users can refer generated workout for each SOP calculation to learn how to solve KMAP for 4 variables manually.
What is 4 Variables Karnaugh's Map?
4 Variables Karnaugh's Map often known as 4 variables K-Map. It's an alternate method to solve or minimize the Boolean expressions based on AND, OR & NOT gates logical expressions or truth tables. The four variables A, B, C & D are the binary numbers which are used to address the min-term SOP of the Boolean expressions. The gray code conversion method is used to address the cells of KMAP table.
The min-term SOP is often denoted by either ABCD, 1s & 0s or decimal numbers. For example, the Boolean expression y = ∑{2, 6, 9, 11, 15} represents the place values of the respective cells which has the higher values (binary 1s). The y = ∑{2, 6, 9, 11, 15} can also be represented by y = ∑{0010, 0110, 1001, 1011, 1111} or y = ∑{ABCD, ABCD, ABCD, ABCD, ABCD}
A is the most significant bit (MSB) and B is the least significant bit (LSB). Each variable A, B, C & D equals to value 1. Similarly, each inverted variable A, B, C & D equals to 0. Any 4 combinations of A, B, C, D, A, B, C & D represents the place values of 0 to 15 to address the cells of table in KMAP solver.
For example, the combinations ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD & ABCD represents the binary values of 0000, 0001, 0010, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 & 1111 respectively. The numeric or decimal equivalent for the combinations A, B, C, D, A, B, C & D represents the cell or place values from 0 to 15 in the table of K-Map solver. For example, the combinations ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD, ABCD & ABCD represents 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 & 15 respectively.
Users may refer the below details to learn more about 4 variables Karnaugh's map or use this online calculator to solve the SOP or generate the complete work for minimum SOP for 4 variables A, B, C & D.
How to Solve 4 Variables KMAP?
Users may refer the below rules & step by step procedure to learn how to find the minimum sum of products (SOP) for the Boolean expression using 4 variables A, B, C & D. When you try yourself solving the min-term SOP of for 3 variables, Users can use this online Karnaugh's map solver for 4 variables to verify the results of manual calculations.
step 1 Addressing the cells of KMap table
When using KMAP solver, generally users should be careful while placing the min-terms. Because, the addressing of min-terms in KMAP table is bit different. The order of the cells are based on the Gray-code method. Refer the below table & information gives the idea of how to group the KMAP cells together. For four variables, the location of the the cells of KMAP table as follows
In Binary Form
Row 1: 0000, 0001, 0011, 0010
Row 2: 0100, 0101, 0111, 0110
Row 3: 1100, 1101, 1111, 1110
Row 4: 1000, 1001, 1011, 1010
| 0000 | 0001 | 0011 | 0010 |
| 0100 | 0101 | 0111 | 0110 |
| 1100 | 1101 | 1111 | 1110 |
| 1000 | 1001 | 1011 | 1010 |
Row 1: 0, 1, 3, 2
Row 2: 4, 5, 7, 6
Row 3: 12, 13, 15, 14
Row 4: 8, 9, 11, 10
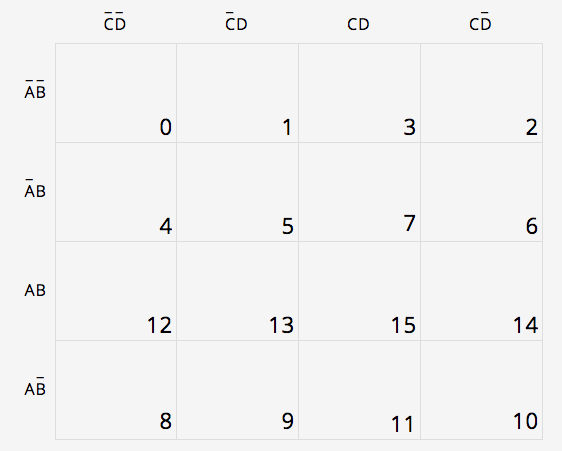
In Variable (A, B, C & D) Form
Row 1: ABCD, ABCD, ABCD, ABCD
Row 2: ABCD, ABCD, ABCD, ABCD
Row 3: ABCD, ABABCD, ABCD, ABCD
Row 4: ABCD, ABCD, ABCD, ABCD
step 2 Write the Boolean expression in the SOP form. Place 1s for those positions in the Boolean expressions and 0s for everything else.
step 3 Group the 1s. The counting of 1s in the group should be in the form of 23, 24, 22 and 21. Therefore you can't group single 1s, three 1s, five 1s, six 1s, seven 1s, nine 1s, ten 1s, eleven 1s, twelve 1s, thirteen 1s, fourteen 1s & fifteen 1s. The possible combinations of grouping are sixteen 1s, eight 1s, four 1s and two 1s together.
step 4 When grouping of 1s the first and last columns are considered adjacent to each other. Similarly, the first & last rows are considered adjacent to each other. The four corner cells of the KMAP table also considered as adjacent to each other.
step 5 Check for sixteen 1s group and encircle the combination, if any.
step 6 Check for eight 1s group and encircle the combination, if any.
step 7 Check for four 1s group and encircle the combination, if any.
step 8 Check for two 1s group and encircle the combination, if any.
step 9 Find the appropriate product term for each combinations.
step 10 Add all the product terms brings the Minimum SOP of the given Boolean expression
